本文共 4864 字,大约阅读时间需要 16 分钟。
对于《编程之美》上没有提供答案和提示的1.18和4.11两节,本文将综合网络上已有的部分资料,深入挖掘解题思路,并对目前尚未找到满意答案的1.18节问题2给出算法解答。阅读本文需要了解古典概型( / )和组合数( / )的含义,以及扫雷游戏中的各种符号。
《编程之美》上关于扫雷的概率有两道题:1.18挖雷游戏和4.11扫雷游戏的概率。后者在网上已经有了令人满意的解答,前者我还没发现,相关内容也很少。经过近一天的研究,提出了一个自己的解法。这篇博文的写作过程,同时也是我整理思路的过程。可能有的读者还没有看过这两道题,或者看了之后记不大清楚了,先把两个问题贴在下面:
1.18 挖雷游戏

问题1:如果想给游戏增加一个功能键,点击就能查看剩余所有未标识的方块是否有地雷的概率。如何实现?
问题2:如果上一个问题太难了,可以先让程序先标识所有有地雷的方块。
4.11 扫雷游戏的概率

在一个16*16的地雷阵中,有40个地雷。用户点击了两下,出现如图4-21的局面。分析图4-22所示的这个局部。
问题1:当游戏中有40个地雷没有发现时,A、B、C三个方块有地雷的概率(P(A),P(B),P(C))各是多少?
问题2:这个局面共有16*16=256个方块,P(A)、P(B)、P(C)的相互大小关系和当前局面中总雷数有关系么?比如从10个逐渐变化到240个,三者曲线如何变化、会不会相交?(建议用Matlab做解)
1.18节的问题2比较好解,而且可以同时标记必然没有地雷的方块;但问题1就困难了,暂且放一边;读了4.11节之后,会发现解4.11节的方法是可以用来理解1.18节的问题的。本文的主要方法就是使用网络上对4.11节提供的解法和1.18节问题2的辅助功能,来完成问题1的解答。
先要明确地强调一点,1.18节的问题1、2与一些所谓的自动扫雷算法是不同的:对于确定为无雷的方块,并不做点击动作;也即仅作概率分析,而不实际地翻开来确认并获得更多信息。因此,有的自动扫雷算法可能每次并不是选择无雷概率最大的方块,包含了一些启发式的尝试。而这里将会对当前状态的所有方块是否有雷的概率进行分析。比如,我觉得这就是个似是而非的自动扫雷解法,要保持当前状态来标注概率,又没让你挖开看看,你知道的太多了,不对,应该是你做的太过火了。
为了便于阅读,我将一些定义(包括我自己的定义)做成了锚点,如果阅读时忘记了前面的含义可以点击链接来查看。
这里先引入“8邻接”的定义。这个定义来源于图形学,如下图,像素P周围的这8个像素就是P的8邻接像素。对应于扫雷问题,同样的可以对一个方块定义它的8邻接方块。
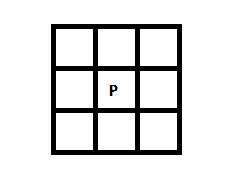
分析:
待标识概率的方块可以根据是否与已经标识的方块是的分为两种,如果是,称之为“邻接方块”,反之则是“非邻接方块”。前者可以按照已标识的方块提供的信息来辅助判断,后者只能取平均概率。对应于原书的例图,“”是两条黑线之间、既未挖开也未标记为有地雷的方块:

对于这两种方块,其有地雷的概率计算方法是不一样的,下面会逐一分析。
为了简化原图,同时解答1.18节问题1,先对必然有雷(即P(此方块有雷)=1)和必然无雷(即P(此方块有雷)=0)的方块进行标识,并且把用旗子标识为“有雷”的地区当作已知是有雷的方块。步骤如下:
(1)(去掉插旗子的方块)把这张图中已经标识为有雷的区域周围8个邻接区域计数减1,并把标识为雷的区域的雷挖掉。同时,对于从1减为0的方块,还要把它8邻接的所有未标识方块标为无雷。这个操作在解问题2之后可以用来进一步转化,从而解决问题1。
等价转化如下图,其中红色方块是经过转化的区域,红色方块且不含数字的标识此方块已无可用信息。具体来说它是由三种方块转化而来:
原先标有数字的,此时它的区域雷已排完;
原先是雷的,将其有雷概率标记为1;
原先无雷的,将其有雷概率标记为0。
注意:它是一种新的已标识方块,而不是是否有雷未确定的未标识方块。

(2)(标记必有雷和必无雷的方块)对所有不为0的区域,先计算周围方块必有雷的方块。判断规则:标为“x”的方块如果有x个的未标识方块,那么必有雷。同时,由于这是由逻辑判断得出的必有雷的区域,不是先前插上旗的,游戏剩余雷数计数器没有变化,需要记录推理出的雷数,并在剩余雷数中减去。
(3)重复(1)(2)的转化,直到标识完毕。在这个过程中,所有地雷概率为0和1的邻接方块已经被处理且标记,问题2得到求解。上图转化为:

并且,在这个过程中标记P(此块有雷)=1的方块一共10个,加上之前扫出的3个,那么40个雷还剩下27个。
这里再次强调,虽然有的方块在处理中标记为P(此块有雷)=0,即必然无雷,但这只是逻辑推理,并不代表我们真的点开了这个方块,它实际的数字是未知的,本身并不能提供周围的雷数信息,只能间接地提示它的8邻接方块的中少了一颗雷而已。
(4)接下来是处理最后一部分,也即P(此方块有雷)非0非1的部分。这里借鉴了一个解答《编程之美》问题4.11思路,原内容来自,但是这个页面我是打不开的,好在转载的人多,比如。另外还有一篇可以参考。
先简单阐述一下其思想。(如果这部分没看懂没关系,看懂上面链接的两篇就可以理解后面的思路):
“子雷区”定义为所有已知信息方块的中所有未挖开未标记方块以及这些已知信息方块的并集,例如以下几个图中的是黑框标出的部分,也是我在上面两条黑线包围的部分中未挖开未标记的部分。可见,“”和“”是类似的,只不过""描述的是这些方块的总体外加一些已知信息,""描述的是个体。下面你会看到使用这个定义的方便之处。

思想:
对于M大小的雷区,其中共有N个雷;已知信息和待判断位置位于一个M'大小的,先分析一共可能有多少个雷;对于每一种雷数,分析其分布的情况总数,在乘以余下的雷在之外的分布情况,其和就是所有的分布情况。待判断位置有雷的概率是它在这些情况中有雷的情况数/所有分布情况(根据),写成公式如下:

现在继续处理(4)中获得的。标记“?”的定义为“结合点”,对它讨论可以把一个复杂的子雷区分成多个简单的。比较巧合的是,《编程之美》1.18这个图,先假设再分情况讨论时会发现有种情况是不成立的,另一种情况只有唯一的可能:

这里举一个和上文图不同的例子说明分别求解的过程。先做出“无雷”假设的假设后,把分为这样两个不相交的:

这时,要求解A处有雷的概率就稍微简单了些。与单独求解一个区域中点是否有雷的概率相比,这些之间的关系是:
所有的雷数+非的雷数+已确定是雷的雷数 = 总雷数。
利用从上述两篇博文中获得的思路,分析如下(这部分的公式是在Word里打的,HTML编辑器玩的不熟,直接截了个图粘上来):

对于不在任何一个的其余所有点,取任一个点X进行分析:

如果结合点分情况讨论,那么计算方法类似,可以表示为:

这样,对于原图中所有点是否有雷的概率,都能给出了。
这下所有点的概率都能求了,似乎1.18节问题1也能解决了。对(1)(2)(3)这三步是这样的,维护好包含有用信息的方块和的数据结构,这么标出来所有P=0和P=1的方块是不难的,然而第 (4)步就犯难了:如何把划分成多个?怎么找?
先回避这个问题,让计算机扬长避短,直接在未划分的搜索所有可能的地雷分布情况数,并统计在特定位置有雷的情况数,概率也就能算出来了。这时的子雷区已经很小了,处理起来不会很慢,不过要注意不能忽略子雷区以外的中地雷的分布情况。
如果非要直面这个问题,让计算机像人一样找、划分、按结合点分情况计数当然也可以,但是编码难度大,计算也未必快。可以注意到,与含有信息的已挖开方块相连的其实最多只有一层,并且是一条直线。如果一个含有信息的已挖开方块与两层相连,那么相连的地方就是待讨论的点,如下图所示,红色和蓝色是两条的一层,紫色是。接下来就是像人一样分情况讨论了,但由于实际划分很复杂,而且这个所谓的讨论其实还是让计算机去进行可能情况的搜索,可能性能还不如上面的直接去搜索快一些。另外,我这里给出的规律是自己总结的,不确定是否有疏漏,可靠性有限。
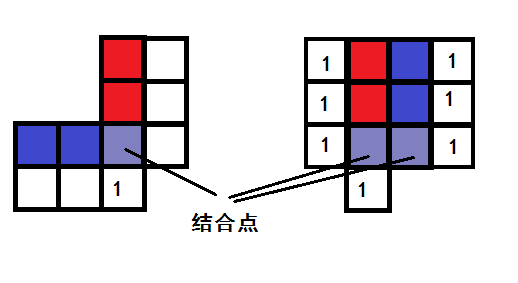
具体的编码就略过了,主要过程是简化原图+搜索算法。按照(1)~(4)步,完全可以写出伪代码框架。
另外预先设计了几个FAQ,当然各位看官如果有什么问题,不要吝惜留言啊!
Q:1.18节标题是“挖雷游戏”,4.11节标题成了“扫雷游戏”,居然不一样!
A:其实这也是我想吐槽的地方:前后不一致,《编程之美》里可是不少,从代码的语言到这小小的标题。
Q:既然有的方块是否有雷能直接判断出来,为什么不挖开从而获得更多信息?
A:这个问题我在正文里强调了两遍了,直接点击跳转过去再读一遍吧。
Q:在4.11中,按3*5区域中有3个雷还是2个雷进行了分情况计数。为什么不用全概率公式(/)?
A:P(A)=P(A|B1)*P(B1) + P(A|B2)*P(B2) + ... + P(A|Bn)*P(Bn),A={A点有雷的概率},Bi={3*5区域中有i个雷的概率},
嗯,看上去很清楚,P(A|Bi)是容易计算了。但是P(Bi)你怎么获得?
Q:为什么对一些定义提供了两个链接?
A:事实上我觉得文中出现的几个定义,百度百科比维基百科阐述的清楚一些。当然有的人不喜欢百度,为了照顾他们的情绪我把维基百科中的定义也附上了。
Q:分析了大半天,最后还是用搜索的方法,真失望。
A:是啊,我也有点失望。但我已经尽力剪枝了,剪到步骤(4) 才权衡是更精细的剪枝开销大还是从这里开始搜索开销大。毕竟结合点的情况太多了,没有进行很简单的抽象。这还是比一开始就搜索要好很多了吧?
Q:我需要的是源代码……
A:其实我可以直截了当地告诉你,博主在windows编程方面非常之poor,以至于现阶段是不可能给你写出源代码的。自己努力吧!当然,如果你搞定了,记得把源码发给我一份^ ^
Q:打不开,那些转载里的图片也看不了,更不会用MATLAB,可还是想看看4.11的三条曲线。
A:这个希望还是能满足的。不过注意到由于地雷数N是离散的,实际上绘出来的是散点图,如下:
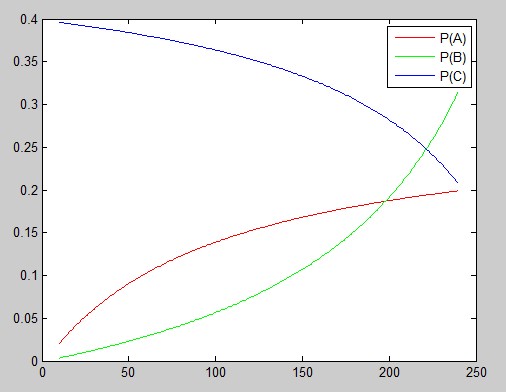
我甚至把MATLAB代码都给你了,直接粘到m文件里就能重现这个图像:
n = 10:1:240; m = 256; %P(A) p1 = (2*n -4)./(3*m+7*n-56); plot(n,p1,'r') hold on %P(B) p2 = (n -2)./(10*m-7*n-126); plot(n,p2,'g') hold on %P(C) p3 = (20*m -17*n-246)./(50*m - 35*n - 570); plot(n,p3,'b') legend('P(A)','P(B)','P(C)')
不过要注意的是,在图像中,P(B)看上去与P(A)和P(C)相交,但真的是这样么?别忘了这三条其实不是连续的曲线,而是离散的点的连线。
令P(A) = P(B),解得N1 = 2,N2 = 4196/21,都不是10至240之间的整数,所以P(A)和P(B)其实没有公共点。
再看看P(B)和P(C),这里解方程比较复杂,直接把图像放大了看,交点似乎是221。带入P(B)和P(C)的表达式,二者不相等,只是很近似。
结论是曲线看上去是相交的,但实际上并没有公共点。怎么样,没有被你的眼睛欺骗吧?
Q:博主,你的XX式子中的XX算错了/扫雷图中XX格分析错了。
A:本文中所有式子和图形标记我都进行了两遍计算/检查了两遍,虽然仍有可能有遗漏的地方,不过也请您先验证一下自己的论断吧,如果确实有错我会改正的。
本文转自五岳博客园博客,原文链接:http://www.cnblogs.com/wuyuegb2312/p/3163833.html,如需转载请自行联系原作者
